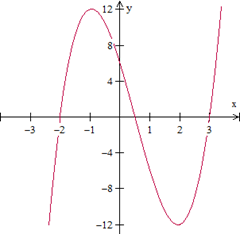
Two of the roots of the equation 
are 
and 
. Find the third root of the equation.
Source: NCTM Mathematics Teacher, August 2006
Solution
Let 
be the third root of the equation. We write the equation in factored form
Multiply the right-hand side
Compare the coefficients of 
Answer: 
Alternative solution 1
Consider a general polynomial of third degree with roots 
and coefficients 
Multiplying out the product on the right-hand side yields
provided that 
Divide 
by 
Third root = 
Alternative solution 2
Substitute the value of 
into the equation
Substitute the value of 
into the equation
Multiply Eq. 
by 
and add to Eq. 
——————–
Substitute the value of 
into Eq.
We now have the cubic equation 
with two known roots 
. We can find the third root either by long division or by synthetic division: 
.
We can also graph the equation to find the third root
