Note: At first I thought this was going to be really straightforward, but then applying it ended up being more time consuming (in which time consuming == fun).
Some of these are obvious, some are refreshing, and some directly apply to data types.
- Simple, Counting numbers. They begin at 0 (or 1, depending on weird ISO standards)
- Just positives, no negatives
- Use these if you’re going to count things: 4 beans on one hand, and 3 beans on the other, makes for 7 beans total.0
Obvious Fact: The sum of any two natural numbers is also a natural number.
Fun Fact: The subtraction of two numbers may yield a natural number or an integer.
Integers ℤ = {..., -2, -1, 0, 1, 2, ...}
- A number with no decimals or fractions, that goes in positive and negative
VEX data type: int
Rational Numbers ℚ = {2/3, 5/2, 1.5, 3.14, .001}
- Integers with decimals/fractions
VEX data type: float
VEX tip: When doing maths operations, it’s important to specify some variables are floating in order to math accordingly.
Example:
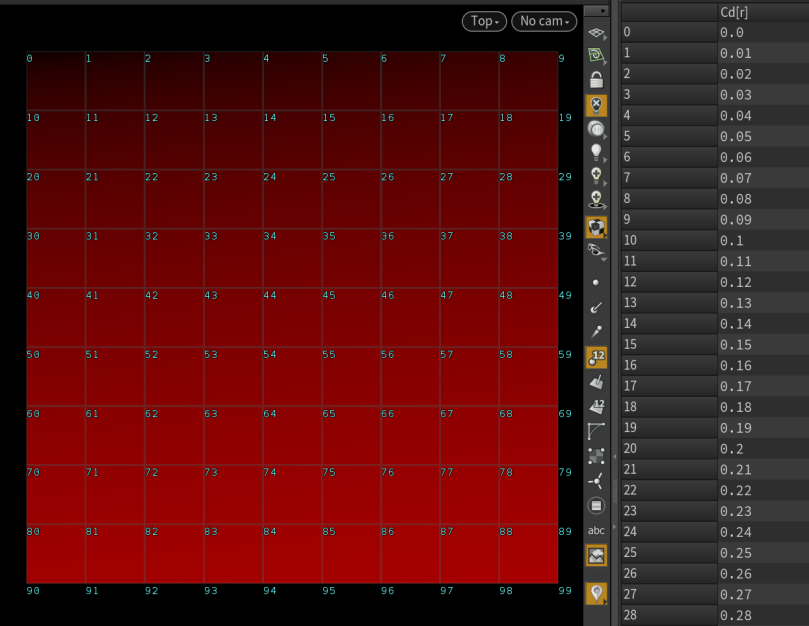
A point wrangle with:
@Cd = float(@ptnum)/@numpt //@ptnum is the point number //@numpt is the total number of pointsyields a nice gradation, since you’re telling VEX that @ptnum is a floating variable, otherwise VEX implies that it is an integer. A gradient is basically just a series of ordered Rational Numbers/float values.
Similarly:
@Cd = float(@ptnum)/@numptyields values of 0 (color data of black) since it’s dividing an integer by an integer, giving us no rational/floating data. Again, the reason for this is because VEX implies/assumes that the variable of @ptnum is an integer.
Download the example file here.
Obvious Fact: Dividing a rational by a rational gives you a rational result.
Irrational Numbers






