A no-brainer, but if you put it into a number line and think about it as 2D lines/splines:
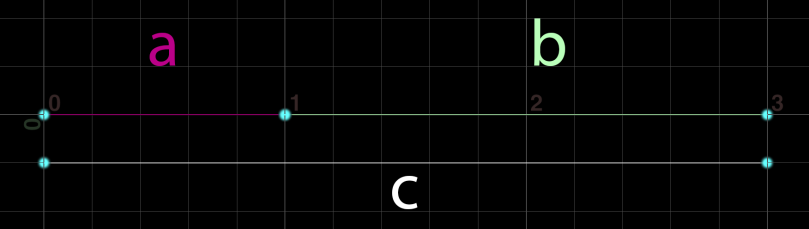
The resulting line length (c) is the equal to the sum of the lengths of the elements (a, b). Ignore that the resulting line (c) is offset by one unit. Don’t nitpick about Cartesian planes just yet.
Addition is commutative, which means
a + b = b + a
Addition is also associative,meaning you can compute in any order and get the same answer:
(a + b) + c = a + (b + c)Subtraction
Quite literally the inverse of Addition.
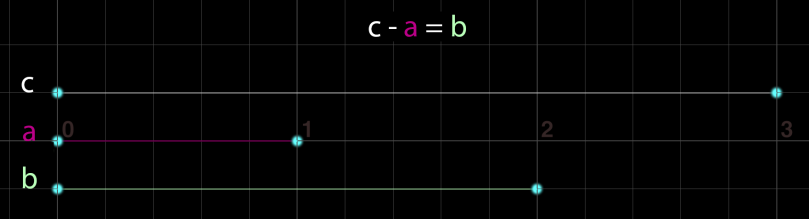
Multiplication
An easy way to put it is Multiplication is simply repeated addition:
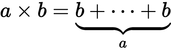
The inverse of Multiplication.
a × b = c, then a = c ÷ bExponentiation
When you multiply a number by itself many times.
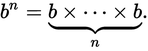
b is called the base, and n is called the exponent, which in practice is:
- b raised to the n-th power
- b raised to the power of n
- the n-th power of b
Example:
x2x2 = (xx)(xx) = xxxx = x4And in VEX / Expressions:
pow(base, exponent)
Negative Exponents: doesn’t mean subtract, but rather divide by.
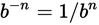
Fractional Exponents: square-root-like operations:
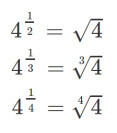
Related:
Square Root in Vex / Expression:
sqrt(number)Square root √x is the inverse operation of x².
Similarly, ⁿ√x (the nth root of x) is the inverse operation of xⁿ.
Note: the nth root of x is a number which, when multiplied together n times, will give x.
This might seem daunting, but break this down and you’ll see (I hope):
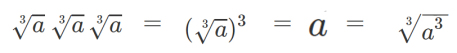
So what was the point of all that last bit?
I don’t have an explicit reason why, but if anything it’ll lay a good groundwork and prove useful if you find yourself translating algorithms or systems from math notation into something useful.
And some gifs just to break up all the monotony of the numbo-jumbo – the preceding functions applied to the rotation of a line made up of 6 points.
 Addition by Frame #
Addition by Frame #
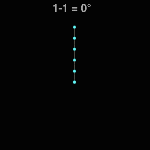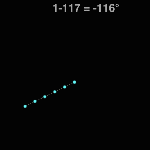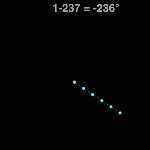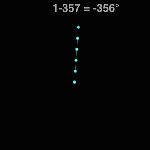 Subtraction by Frame #
Subtraction by Frame #
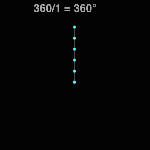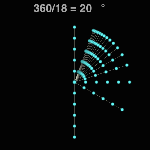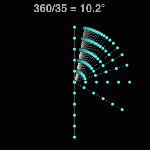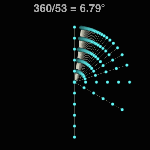 Division by Frame #
Division by Frame #
 Exponentiation of base 1.1 to exponent of Frame #
Exponentiation of base 1.1 to exponent of Frame #
And then to wrap up the most boring and basic of things, there’s the Order of Operations, which can be abbreviated to PEMDAS:
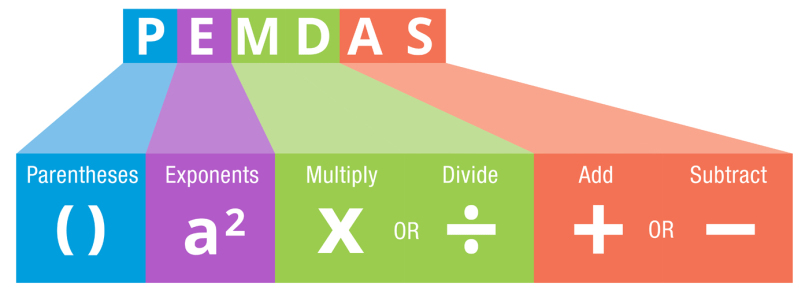
This really shouldn’t need to be said, but I’ve included it for thoroughness sake.
Advertisements Share this:




